cscx的原函数是:ln|tan(x/2)|+C或者ln|cscx-cotx|+C。
∫cscxdx=ln|tan(x/2)|+C,也可写作:∫cscxdx=ln|cscx-cotx|+C。
∫cscx dx =∫1/sinx dx =∫1/[2sin(x/2)cos(x/2)] dx =∫1/[sin(x/2)。
cscx的原函数:ln|tan(x/2)|+C。
secx的原函数:ln|secx+tanx|+C。
C为积分常数。
分析过程如下:求cscx和secx的原函数就是分别对二者不定积分。
∫secxdx =∫secx(secx+tanx)dx//(secx+tanx)=∫(sec²x+tanxs。
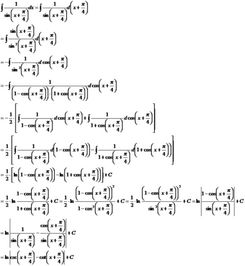
如图
回ln(tan(x/2))
高等数学~~这一步怎么转化的阿?不定积分我会算 主要是这俩三角函数很。=∫sinx/sin^2(x)dx =-∫d(cosx)/(1-cos^2(x))=-1/2∫(1/(1-cosx)+1/(1+cosx))d(cosx)=1/2ln|(1-cosx)/(1+cosx)|+C =ln|(1-cosx)/sinx|+C (根号里面上下同时乘1-cosx)=ln|cscx-cotx|。