两个向量a和b的叉积写作a×b(有时也被写成a∧b,避免和字母x混淆)。
模长:(在这里θ表示两向量之间的夹角(共起点的前提下)(0°≤θ≤180°),它位于这两个矢量所定义的平面上。
)方向:a向量与b向量的向量。
2. 叉积(外积):向量的叉积是一个向量,其方向垂直于原来的两个向量,并且大小与这两个向量构成的平行四边形的面积成正比。
叉积的表示方式为 "×" 或者 "AxB"。
如果有两个三维向量 A = [A1, A2, A3] 和 B =。
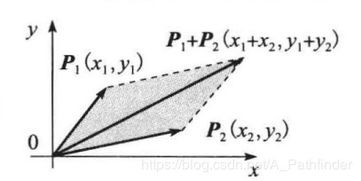
叉乘,也叫向量积。
结果是一个和已有两个向量都垂直的向量。
叉乘结果是一个向量,向量模长是向量A,B组成平行四边形的面积;向量方向是垂直于向量A,B组成的平面(右手螺旋定则)。
与向量对应的量叫做数量(物理学中称标量。
一、叉积与数量积的区别:外积≠叉积(向量的积一般指点乘),一定要清晰地区分开外积(叉积)与数量积(标积),二、叉积(矢积)与数量积(标积)的区别:1、标积/内积/数量积/点积的运算式(a,b和c粗体字,表示。
向量积,数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。
与点积不同,它的运算结果是一个向量而不是一个标量。
并且两个向量的叉积与这两个向量和垂直。
其应用也十分广泛,通常应用于物理。