向量叉乘的几何意义是叉积等于由向量A和向量B构成的平行四边形的面积。
叉乘的运算结果是一个向量而不是一个标量,上述结果是它的模, 向量C的方向与A,B所在的平面垂直,方向用“右手法则”判断。
判断方法如下:右手手掌张。
点乘的几何意义:可以用来表征或计算两个向量之间的夹角,以及在b向量在a向量方向上的投影。
叉乘的几何意义:在三维几何中,向量a和向量b的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面。
。
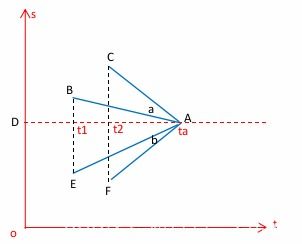
叉乘的几何意义是:如矢量x叉乘矢量y就是右手四指与x方向相同向y方向弯曲,大拇指的方向就是,叉乘结果的方向,大小的x和y所围的面积
点乘的几何意义 可以用来表征或计算两个向量之间的夹角,以及在b向量在a向量方向上的投影。
叉乘的几何意义 在三维几何中,向量a和向量b的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面。
在。
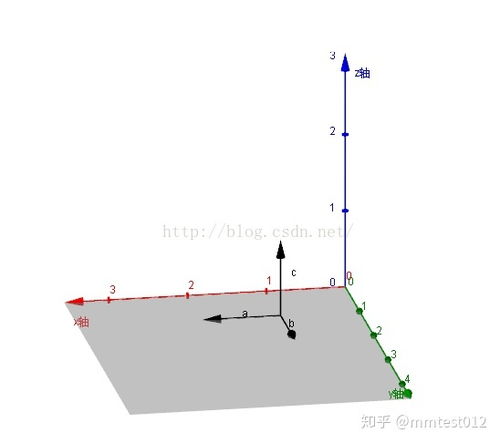
向量的叉乘如X叉乘Y就是一个垂直于X和Y组成的平面的一个向量,方向是这样决定的,右手四指与X的方向相同,大拇指与四指垂直,然后四指按照这样的方向绕,从X开始,经过X与Y的锐角的方向环绕,拇指所指的方向就是X叉乘Y的。