向量积,也称为叉乘或矢量积,是在三维空间中定义的一种向量运算。
它用于计算两个向量之间的叉乘结果,结果是一个新的向量。
向量积的结果向量垂直于原始向量所在的平面,并且其大小与原始向量的长度和夹角有关。
设有两个向量。
A=(x1,y1,z1),B=(x2,y2,z2),则A与B的向量积为
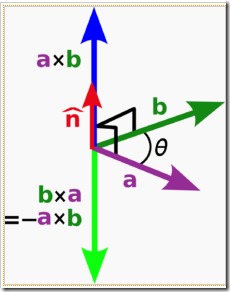
向量积(叉乘)a × b 是两个向量 a 和 b 的向量运算,其结果是一个新的向量,垂直于原来两个向量所在的平面。
向量积的大小(模长)等于两个向量的模长的乘积与它们之间夹角的正弦值的乘积。
向量积的方向满足右手法则。
向量乘向量等于向量积。
向量积,数学中又称外积和叉积,物理中称矢积和叉乘,是一种在向量空间中向量的二元运算。
与点积不同,它的运算结果是一个向量而不是一个标量。
并且两个向量的叉积与这两个向量和垂直。
其应用也十。
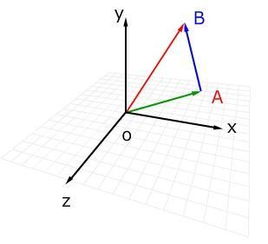
向量的向量积运算律:a×b=-b×a;(λa)×b=λ(a×b)=a×(λb);(a+b)×c=a×c+b×c.注:向量没有除法,“向量AB/向量CD”是没有意义的。
向量的三角形不等式:∣∣a∣-∣b∣∣≤∣a+b∣≤。