四面体的体积公式V=1/6*abc(sin^2α+sin^2β+sin^2γ+2cosαcosβcosγ-2)^(1/2)。
先取定一个面为底面,设它的面积为s,再过另一个不在底面的顶点作底面的高,算出高为h那么四面体的体积就是hs/3。
正。
四面体体积公式是V=Sh/3。
四面体一般指三棱锥,三棱锥固定底面时有一个顶点,不固定底面时有四个顶点。
正三棱锥不等同于正四面体,正四面体必须每个面都是正三角形。
四面体作为最简单、最基本的几何体。
若四面体的外接球球。
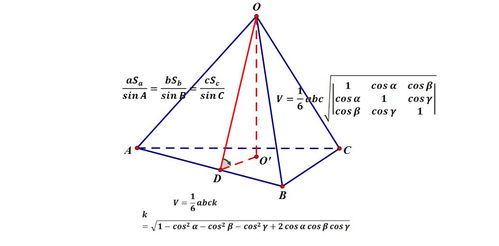
V=Sh/3。
四面体一般指三棱锥,三棱锥固定底面时有一个顶点,不固定底面时有四个顶点。
正四面体就是由四个全等正三角形围成的空间封闭图形。
它有6条棱,4个顶点。
正四面体是最简单的正多面体。
当其棱长为a时,其体积等。
四面体体积公式不是1/6abc,四面体就是三棱锥,以任意两坐标轴所在面为底面,则另一坐标轴为高,利用锥体体积公式可得V=Sh/3=1/2×ab×c/3=abc/6。
四面体是由不在同一平面的四点所连接成的四个三角形包围起来的立体。
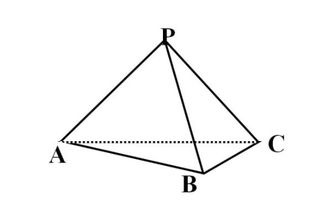
正四面体必须每个面都是正三角形)。
正四面体的体积公式是√2a_/12,正四面体是由四个全等正三角形围成的空间封闭图形,所有棱长都相等,它有4个面,6条棱,4个顶点,正四面体是最简单的正多面体。