割圆术就是用圆内接正多边形来近似代替圆。
刘徽认为,当圆内接正多边形数无限增加时,其周长即愈益逼近圆周长。
”圆内接正多边形数无限多时,其周长的极限即为圆周长,面积的极限即为圆面积。
这里包含了最早的极限概念和直线。
割圆术(cyclotomic method)所谓“割圆术”,是用圆内接正多边形的周长去无限逼近圆周并以此求取圆周率的方法。
“圜,一中同长也”。
意思是说:圆只有一个中心,圆周上每一点到中心的距离相等。
早在我国先秦时期,《墨经》。
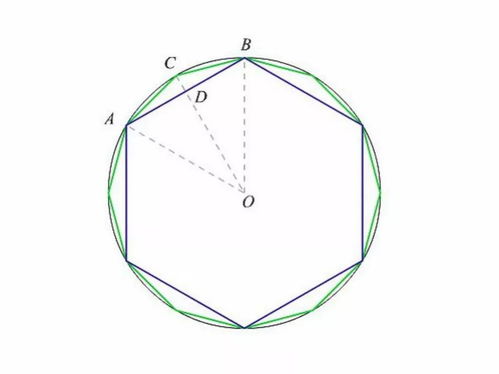
割圆术是以“圆内接正多边形的面积”,来无限逼近“圆面积”。
即通过圆内接正多边形细割圆,并使正多边形的周长无限接近圆的周长,进而来求得较为精确的圆周率。
根据“圆周长/圆直径=圆周率”,那么圆周长=圆直径*圆周率=2。
详细的问题说明,有助于回答者给出准确的答案割圆术(cyclotomic method)所谓“割圆术”,是用圆内接正多边形的周长去无限逼近圆周并以此求取圆周率的方法。
这个方法,是刘徽在批判总结了数学史上各种旧的计算方法之后,经过深思熟虑才创造出来的一种崭新的方法。
中国古代。
割圆术是刘徽发明的。
3世纪中期,魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法,所谓割圆术,就是不断倍增圆内接正多边形的边数求出圆周率的方法。
特点 刘徽割圆术简单而又严谨,富于程序性,。