子集是一个数学概念:如果集合A的任意一个元素都是集合B的元素,那么集合A称为集合B的子集。
符号语言:若∀a∈A,均有a∈B,则A⊆B。
如果集合A的任意一个元素都是集合B的元素(任意a∈A则a∈B),那么。
子集,为大集合中一部分的集合,故亦称部分集合。
[编辑本段]定义对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,我们就说集合A包含于集合B,或集合B包含集合A,也说集合A是集合B的子集。
如果集合A的任何。
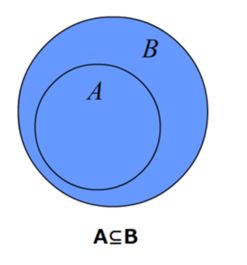
“子集是一个数学概念:如果集合A的任意一个元素都是集合B的元素,那么集合A称为集合B的子集。
符号语言:若∀a∈A,均有a∈B,则A⊆B。
”如果集合A的任意一个元素都是集合B的元素(任意a∈A则a∈B),。
可以这样理解:1. 子集:如果一个集合中的所有元素都能够在另一个集合中找到,那么前者就是后者的子集。
2. 真子集:如果一个集合中的所有元素都在另一个集合中找到,但后者中存在一些元素不属于前者,那么前者就是后者的。
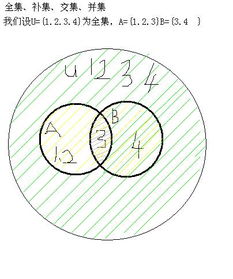
子集就是一个集合中的元素,全部都是另一个集合中的元素,有可能与另一个集合相等。
真子集就是一个集合中的元素,全部是另一个集合中的元素,但不存在相等。
性质 一、根据子集的定义,我们知道A⊆A。
也就是说,。