方差公式:标准差公式:标准差=sqrt(((x1-x)^2 +(x2-x)^2 +。(xn-x)^2)/n)。
性质:设C为常数,则D(C) = 0(常数无波动); D(CX )=$C^2$ D(X ) (常数平方提取,C为常数,X为随机变量)。
标。
方差公式:S^2=〈(M-x1)^2+(M-x2)^2+(M-x3)^2+…+(M-xn)^2〉╱n。
标准差公式:样本标准差=方差的算术平方根=s=sqrt(((x1-x)²+(x2-x)²+……(xn-x)²)/(n-1))。
总体标准。
公式:1、方差s=[(x1-x)^2+(x2-x)^2+(xn-x)^2]/n(x为平均数)2、标准差=方差的算术平方根它们的意义:1、方差的意义在于反映了一组数据与其平均值的偏离程度;2、方差是衡量随机变量或一组数据时离散程度的度。
标准差=方差的算术平方根=s=sqrt(((x1-x)^2+(x2-x)^2+(xn-x)^2)/(n-1))。
方差D=(X1-U)*(X1-U)+(X2-U)*(X2-U)+(Xn-u)*(Xn-U)。
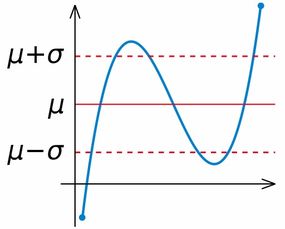
标准差是一组数值自平均值分散开来的程度的一种测量观念。
。

方差的计算公式为S^2=1/n[(x1-x)^2+(x2-x)^2+……+(xn-x)^2]一、方差和标准差的介绍 方差 方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。
概率论中方差用来度量随机变量和其数学期望。