塞瓦定理是指在△ABC内任取一点O,延长AO、BO、CO分别交对边于D、E、F,则 (BD/DC)×(CE/EA)×(AF/FB)=1。
使用塞瓦定理可以进行直线形中线段长度比例的计算,其逆定理还可以用来进行三点共线、三线共点等问题的。
塞瓦定理是指在△ABC内任取一点O,延长AO、BO、CO分别交对边于D、E、F,则 (BD/DC)×(CE/EA)×(AF/FB)=1。
塞瓦(Giovanni Ceva,1648~1734)意大利水利工程师,数学家。
塞瓦定理载于塞瓦于1678年发表的《直线论》。
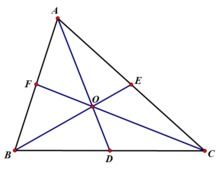
塞瓦定理 塞瓦定理 设O是△ABC内任意一点,AO、BO、CO分别交对边于D、E、F,则 BD/DC*CE/EA*AF/FB=1 证法简介 (Ⅰ)本题可利用梅内劳斯定理证明:∵△ADC被直线BOE所截,∴ CB/BD*DO/OA*AE/EC=1 ①。
塞瓦定理是指在△ABC内任取一点O,延长AO、BO、CO分别交对边于D、E、F,则 (BD/DC)×(CE/EA)×(AF/FB)=1。
按角分 判定法一:1、锐角三角形:三角形的三个内角都小于90度。
2、直角三角形:三角形的三个内角。
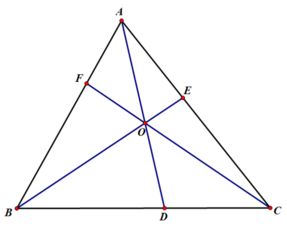
塞瓦定理 设 分别是 三边 或其延长线的点,若 三线平行或共点,则 .塞瓦定理的逆定理 设 分别是 三边 或其延长线的点,若 则 三直线共点或三直线互相平行.将两个定理合写为: 设 分别是 三边。