x^3-1 =x^3-x^2+x^2-x+x-1 =(x^3-x^2)+(x^2-x)+(x-1)=x^2*(x-1)+x*(x-1)+(x-1)=(x-1)*(x^2+x+1)即x^3-1可因式分解为x^3-1=(x-1)*(x^2+x+1)。
因式分解方法灵活,技巧。
x^3-1=(x-1)(x^2+x+1)。
推导过程 一、方法一(立方差公式法)立方差公式:a^3-b^3=(a-b)(a^2+ab+b^2)。
因为“1”的任何次方都等于“1”本身,所以自然有1^3=1,所以x^3-1=x^3-1^3。
在立方差。
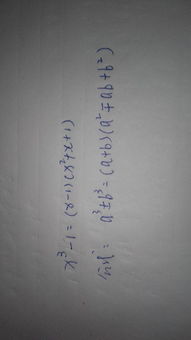
x的三次方减一是x³-1=﹙x-1﹚﹙x²+x+1﹚。
把一个多项式在一个范围(如实数范围内分解,即所有项均为实数)化为几个整式的积的形式,这种式子变形叫做这个多项式的因式分解。
因式分解与解高次方程有密切的。
x的三次方减一等于﹙x-1﹚﹙x²+x+1﹚。
把一个多项式在一个范围内化为几个整式的积的形式,这种式子变形叫做这个多项式的因式分解。
1、立方差公式也是数学中常用公式之一,在数学研究中该式占有很重要的地位,甚至。
x的三次方减一等于﹙x-1﹚﹙x²+x+1﹚。
把一个多项式在一个范围(如实数范围内分解,即所有项均为实数)化为几个整式的积的形式,这种式子变形叫做这个多项式的因式分解。
1、因式分解与解高次方程有密切的关系,。