余切的定义是cotx = cosx / sinx。
而cotx = 1 / tanx是由余切定义推导出来的。
只有在正切和余切都有定义的前提下才成立。
cot(cotangent)是三角函数里的余切三角函数符号,此符号在以前写作ctg。
cot坐标系表示:cotθ=x。
带余切(cot)、正割(sec)和余割(csc)是三角函数的倒数。
1. 带余切(cot):带余切是正切(tan)的倒数。
在一个直角三角形中,带余切定义为邻边(直角边)与对边(斜边上除直角边之外的部分)的比值。
带余切的公式。
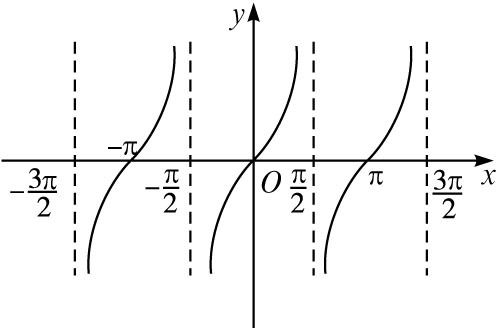
对于任意一个实数x,都对应着唯一的角(弧度制中等于这个实数),而这个角又对应着唯一确定的余切值cotx与它对应,按照这个对应法则建立的函数称为余切函数。
余切用"cot+角度"表示,如:30°的余切表示为cot30°;角A的余切。
cotx余切的图像如下,余切与正切互为倒数,任意角终边上除顶点外的任一点的横坐标除以该点的非零纵坐标,角的顶点与平面直角坐标系的原点重合,而该角的始边则与正x轴重合。
用“cot+角度”表示。
余切函数的图象由一些隔离的。
余切函数公式是:cot(A)=b/a。
其中a为对边,b为临边,c为斜边。
cot坐标系表示:cotθ=x/y,在三角函数中cotθ=cosθ/sinθ,当θ≠kπ,k∈Z时cotθ=1/tanθ(当θ=kπ,k∈Z时,cotθ不存在),cotA=∠A。