i的三次方是-i。
i^1 = i,i^2 = - 1,i^3 = - i,i^4 = 1。
i^n具有周期性,且最小正周期是4。
i^4n=1,i^4n+1=i,i^4n+2=-1,i^4n+3=-i。
由于虚数特殊的运算规则,出现了符号i。
在数学里。
知道i的平方等于-1,i的4次方等于1,却不知道i等于多少?i的3次方等于多。一般地,i^(4n+1)=i, i^(4n+2)=-1, i^(4n+3)=-i, i^(4n+4)=1。
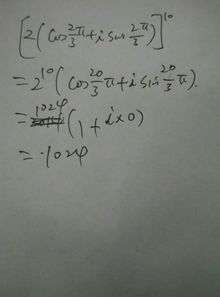
i的三次方等于-i。
次方最基本的定义是:设a为某数,n为正整数,a的n次方表示为aⁿ,表示n个a连乘所得之结果,如2⁴=2×2×2×2=16。
次方的定义还可以扩展到0次方和负数次方等等。
在电脑上输入数学公。
i=3,i的三次方就是3x3x3=27。
二项展开式,这是伟大的科学家牛顿推导出来的,并且他还把指数推广到有理数的范围。
学生阶段基本上只用到正整数指数部分的公式,也就是这篇文章主要讲的这个公式。
有理数指数的牛顿二项。

i的三次方等于-i