平方和公式:1²+2²+3²+。+n²=n(n+1)(2n+1)/6.推理如下:2³-1³=3×1²+3×1+1 3³-2³=3×2²+3×2+1 4³-3³=3×3&#。
平方和Sn= n(n+1)(2n+1)/6,推导:(n+1)^3-n^3=3n^2+3n+1,n^3-(n-1)^3=3(n-1)^2+3(n-1)+1,。2^3-1^3=3*(1^2)+3*1+1,把这n个等式两端分别相加,得:(n+1)^3 -1=3(1^2+2。

平方和公式:n(n+1)(2n+1)/6,即1²+2²+3²+…+n²=n(n+1)(2n+1)/6。
1、1到N的平方和推导:1²+2²+3²+。
。
。
+n²=n(n+1)(2n+1)/6 由1²+2²+3²+。
。
。
+n²=n(n+1)(2n+1)/6 ∵(a+1)³-a³=3a&#。
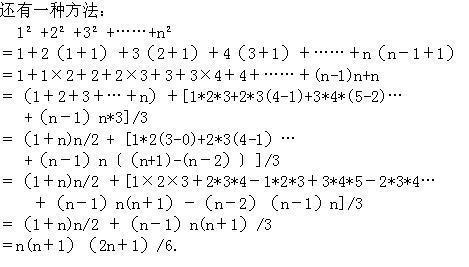
推导过程:(n+1)^3-n^3 = 3*n^2+3*n+1 n^3-(n-1)^3 = 3*(n-1)^2+3*(n-1)+1 ………2^3-1^3 = 3*1^2+3*1+1 以上n条式子相加得 (n+1)^3-1 = 3*(1^2+2^2+……+n^2)+3*(。