三角函数诱导公式口诀如下:诱导公式一共分为下面几组(正切用正弦与余弦的商即可推导),sin(90°-α)= cosα;sin(90°+α)= cosα;cos(90°-α)= sinα;cos(90°+α)= - sinα;sin(270°-α)= - cos。
诱导公式口诀:“奇变偶不变,符号看象限”。
1、诱导公式是数学三角函数中将角度比较大的三角函数利用角的周期性,转换为角度比较小的三角函数。
在四个象限的符号如何判断,也可以记住口诀“一全正;二正弦(余割);三两切;。
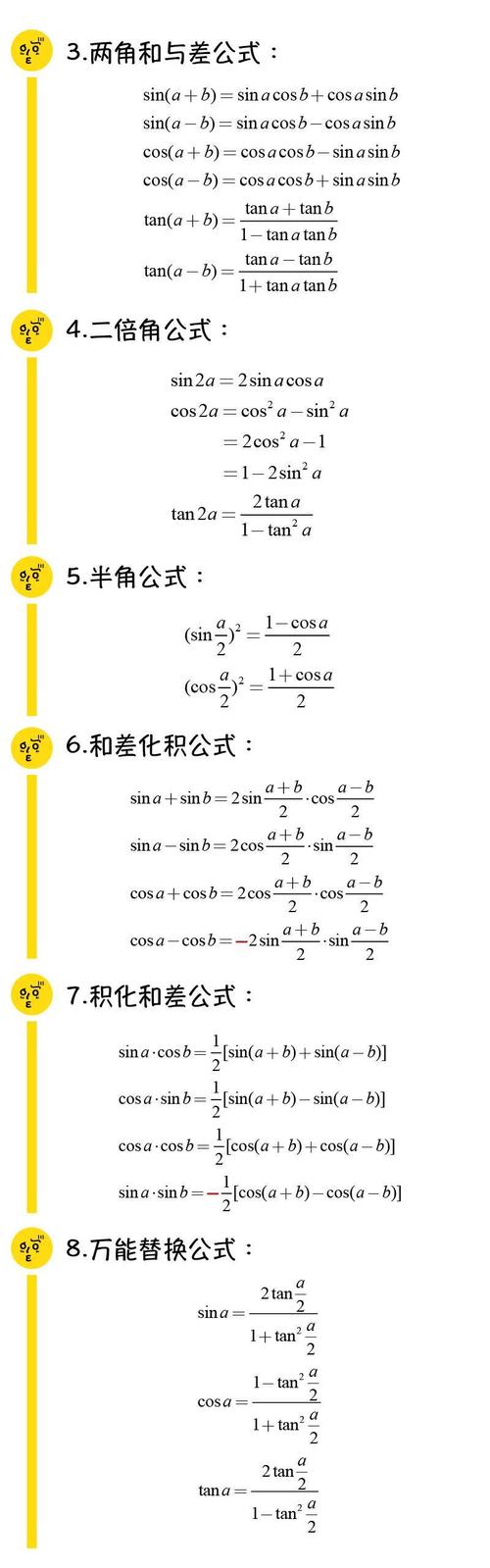
公式一到公式五可简记为:函数名不变,符号看象限。
即α+k·360°(k∈Z),﹣α,180°±α,360°-α的三角函数值,等于α的同名三角函数值,前面加上一个把α看成锐角时原函数值的符号。
上面这些诱导公式可以概括。
2、诱导公式记忆口诀:“奇变偶不变,符号看象限”。
“奇、偶”指的是π/2的倍数的奇偶,“变与不变”指的是三角函数的名称的变化:“变”是指正弦变余弦,正切变余切。
(反之亦然成立)“符号看象限”的含义是:把。
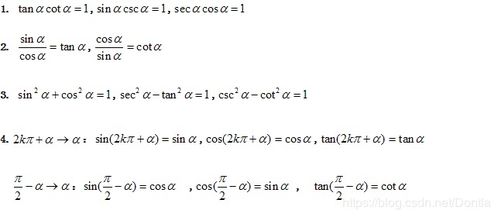
符号看象限是:用诱导公式后函数名的符号与用诱导公式前函数名的符号相同。
例如:sin(3π/2+x)3π/2是π/2的奇数倍,函数名变为cos 3π/2+x(x看作锐角)在第四象限,第四象限正弦为负,因此sin(3π/2+x)=-。